I saw a problem on Twitter the other week, shared I think by Steven Strogatz (@stevenstrogatz): cut a triangle with a line in such a way that the area is cut in half, and also the perimeter. The suggestion was to try a 3-4-5 right triangle. After some effort, I began to doubt there is a solution to the problem; I might not have done the problem correctly, but when I tried to set up equations for the line, they would have solutions representing lines that did not intersect the intended sides.
But I became curious at what would happen if the perimeter is ignored, and a triangle is divided by a line into regions of equal area. My first question is whether all lines that do that pass through a common point. It turns out they don't. I then wondered what the envelope curve would be of all the lines that divide a triangle in half by area. With some work, I determined that the envelope curve would be a piecewise curve composed of arcs of hyperbolas (for a 3-4-5 right triangle, at least, but I was pretty sure this would be true in general).
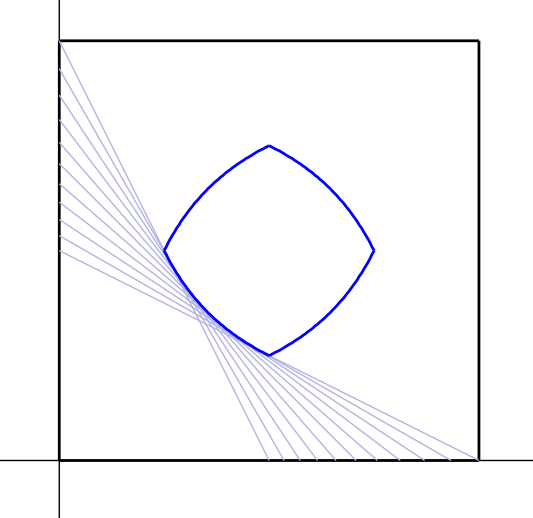
I then thought of other regions. A square is not interesting; any line that divides it in half by area will go through its center. But then I thought, what if a square is divided by a line in such a way that one side of the line always has (say) one-fourth of the area, and the other side has three-fourths of the area of the square. I saw that again, a curve composed of hyperbolic arcs is the envelope curve of all such lines. Some careful work verified this, and pinned down the exact curve.
So here are renderings of the envelope curve. The setup is as follows: This is a unit square, \([0,1]\times[0,1]\). Each gray line divides the square into two regions, one of area \(\tfrac14\), and one of area \(\tfrac34\). All of these lines are tangent to the envelope curve, which turns out to be an arc of the hyperbola \(xy=\tfrac18\). The arc connects the points \((\tfrac14,\tfrac12)\) and \((\tfrac12,\tfrac14)\). The other three arcs of the envelope curve are reflections of the arc just described across \(x=\tfrac12\) and/or \(y=\tfrac12\).

Now the endpoints of each of the four hyperbolic arcs have the property that lines through them that connect opposite sides of the square will also divide the square into two regions of areas \(\tfrac14\) and \(\tfrac12\) respectively. So any line that is tangent to the envelope curve, or passes through the vertices without crossing the region bounded by the curve, will cut the square into two regions of the aforementioned areas.
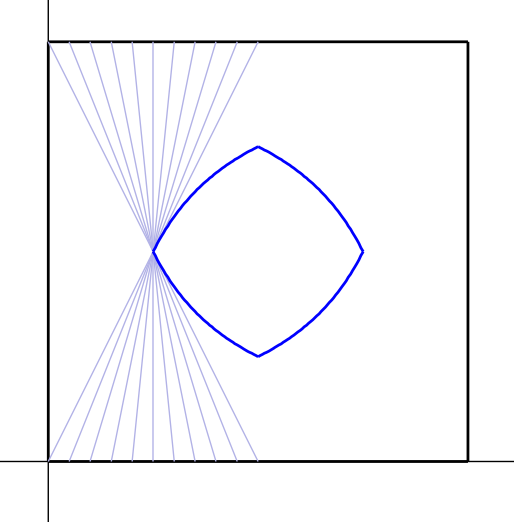
Of course, at this point, I haven't tried to find out if anyone has done this before; I would be very surprised if not. But I think this might be a fun project for a student — there are many possible directions to explore: different polygons, regions with smooth boundary curves, non-convex regions.